Monte-Carlo-Simulation

Zusammenfassung

Unter Risikoquantifizierung versteht man die quantitative Beschreibung eines Risikos und – als nächsten Schritt – die Ableitung eines Risikomaßes (einer Kennzahl), die Risiken vergleichbar macht.

Grundsätzlich sollte ein Risiko zunächst durch eine geeignete (mathematische) Verteilungsfunktion beschrieben werden. Häufig werden Risiken dabei durch Eintrittswahrscheinlichkeit und Schadenshöhe beschreibbar was einer sog. Binomialverteilung (digitale Verteilung) entspricht. Manche Risiken, wie Abweichung bei Instandhaltungskosten oder Zinsaufwendungen, die mit unterschiedlicher Wahrscheinlichkeit verschiedene Höhen erreichen können, werden dagegen durch andere Verteilungsfunktionen (z. B. eine Normalverteilung mit Erwartungswert und Standardabweichung) beschrieben. Die wichtigsten Verteilungsfunktionen im Rahmen des praktischen Risikomanagements sind die Binomialverteilung, Normalverteilung und Dreiecksverteilung (Albrecht / Maurer, 2005 und Gleißner, 2011).

Binomialverteilung

Die Binomialverteilung beschreibt die Wahrscheinlichkeit, dass bei n-maliger Wiederholung eines so genannten Bernoulli-Experiments das Ereignis A genau k-mal eintritt. Ein Bernoulli-Experiment ist dadurch gekennzeichnet, dass genau 2 Ereignisse A und B mit Wahrscheinlichkeit p bzw. 1-p auftreten, diese Wahrscheinlichkeiten sich bei den Versuchswiederholungen nicht verändern und die einzelnen Versuche unabhängig voneinander sind. Ein Beispiel für das Auftreten dieser Wahrscheinlichkeitsverteilung ist das mehrmalige Werfen einer Münze.

Ein Spezialfall der Binomialverteilung ist die „digitale Verteilung“. Hier bestehen die zwei möglichen Ereignisse aus den Werten Null und Eins. In Praxis erfolgt hier oft die Beschreibung eines Risikos durch „Schadenshöhe“ und „Eintrittswahrscheinlichkeit“ (innerhalb einer vorgegebenen Periode).

Normalverteilung Die Normalverteilung kommt in der Praxis häufig vor. Dies ergibt sich aus dem so genannten zentralen Grenzwertsatz. Dieser besagt, dass eine Zufallsvariable annähernd normalverteilt ist, wenn diese Zufallsvariable als Summe einer großen Anzahl voneinander unabhängiger, kleiner „Einzelrisiken“ aufgefasst werden kann. Hat ein Unternehmen beispielsweise eine Vielzahl von etwa gleich bedeutenden Kunden, deren Kaufverhalten nicht voneinander abhängig sind, kann man annehmen, dass Abweichungen vom geplanten Umsatz annähernd normalverteilt sein werden. Es ist in einem solchen Fall also unnötig, jeden Kunden einzeln zu betrachten, sondern es kann der Gesamtumsatz analysiert werden. Die Normalverteilung wird beschrieben durch Erwartungswert , der anzeigt, was „im Mittel“ passiert, und Standardabweichung als Maß für die „übliche“ Streuung um den Erwartungswert.

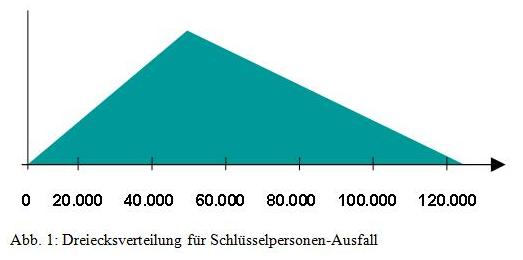
Dreiecksverteilung Die Dreiecksverteilung erlaubt – auch für Anwender ohne tiefgehende statistische Vorkenntnisse – eine intuitiv einfache quantitative Beschreibung des Risikos einer Plan-Variablen, wie z. B. einer Kostenposition. Es müssen lediglich drei Werte für die risikobehaftetete Variable angegeben werden: der Minimalwert a, der wahrscheinlichste Wert b und der Maximalwert c. Dies bedeutet, dass von einem Anwender keine Abschätzung einer Wahrscheinlichkeit gefordert wird. Dies geschieht implizit durch die angegebenen drei Werte und die Art der Verteilung. Die Beschreibung eines Risikos mit diesen drei Werten ähnelt der in der Praxis gebräuchlichen Art der Szenariotechnik, wobei jedoch hier die Wahrscheinlichkeitsdichte für alle möglichen Werte zwischen dem Minimum und dem Maximum berechnet wird. Die folgende Ab-bildung zeigt eine Dreiecksverteilung am Beispiel des Ausfalls von Schlüsselpersonen.

Die Risikoquantifizierung zeigt in diesem Fall einen Schaden von maximal 125.000 €, falls eine Schlüsselperson ausfallen würde. Es kann jedoch auch sein, dass keine erhöhten Kosten entstehen. 50.000 € sind die wahrscheinlichsten Kosten. Der Erwartungswert einer Dreiecksverteilung berechnet sich durch , die Standardabweichung durch .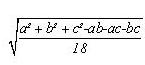

Neben den oben genannten und in der Praxis des Risikomanagements besonders wichtigen Wahrscheinlichkeitsverteilung gibt es eine ganze Reihe weiterer. Für die quantitative Beschreibung von „Extremrisiken“ (wie „Crashs“ oder Naturkatastrophen) kommt beispielsweise die (verallgemeinerte) Pareto-Verteilung zum Einsatz (siehe hierfür weiterführend Zeder, 2007).

Anstelle der unmittelbaren Beschreibung eines Risikos durch die (monetären) Auswirkungen innerhalb einer Planperiode (z. B. eines Jahres) kann auch die Beschreibung durch zwei Wahrscheinlichkeitsverteilungen erfolgen, die dann erst zu aggregieren sind: eine Wahrscheinlichkeitsverteilung für Häufigkeit eines Schadens und eine zweite für die (ebenfalls unsichere) Schadenshöhe je Schadensfall, was bei versicherbaren (ereignisorientierten) Risiken üblich ist. Für die Abbildung komplexerer Problemstellungen kann auch die Kombination von zwei Verteilungen angemessen sein. So kann man beispielsweise das Risiko aus einem Haftpflichtprozess beschreiben durch eine Kombination der Binomialverteilung und der Dreiecksverteilung. Zunächst wird angegeben, mit welcher Wahrscheinlichkeit der Prozess verloren geht (Binomialverteilung). Im zweiten Schritt wird durch die Angabe von Mindestwert, wahrscheinlichsten Wert und Maximalwert die mögliche Schadenssumme spezifiziert.

Für die Bewertung eines Risikos kann man sich orientieren an tatsächlich in der Vergangenheit eingetretenen Risikowirkungen (Schäden), an Benchmarkwerten aus der Branche oder an selbst erstellten (realistischen) Schadensszenarien, die dann präzise zu beschreiben und hinsichtlich einer möglichen quantitativen Auswirkung auf das Unternehmensergebnis zu erläutern sind. Hierbei sind grundsätzlich die Konsequenzen für die Umsatz- und die Kostenentwicklung zu betrachten.

Die bisher im Kontext der quantitativen Beschreibung eines Risikos betrachteten Wahrscheinlichkeitsverteilungen beschreiben die Risikowirkung zu einem Zeitpunkt oder in einer Periode. Die Wirkung vieler Risiken ist allerdings nicht auf einen Zeitpunkt oder eine Periode beschränkt. Um beispielsweise das Wechselkursrisiko adäquat zu erfassen, sollte die gesamte unsichere zukünftige Entwicklung des zugrundeliegenden (exogenen) Risikofaktors, z.B. des Dollarkurses, betrachtet werden. Dabei sind Abhängigkeiten der Risikoauswirkung von Periode zu Periode zu berücksichtigen. So wirkt sich beispielsweise eine (unerwartete) Veränderung des Dollarkurses im Jahr 2011 auch auf das Folgejahr 2012 aus: Der Dollarkurs am Ende von 2011 ist nämlich der Startkurs 2012. Um die zeitliche Entwicklung unsicherer Plangrößen oder exogener Risikofaktoren zu beschreiben, sind daher sogenannte „stochastische Prozesse“ notwendig, die man als „mehrperiodige Wahrscheinlichkeitsverteilungen“ umschreiben könnte.

Stochastische Planung und Risikoaggregation mittels Monte-Carlo-Simulation

Zielsetzung der Risikoaggregation ist nun die Bestimmung der Gesamtrisikoposition eines Projekts oder Unternehmens. Dazu werden die Wahrscheinlichkeitsverteilungen einzelner Risiken zu einer Wahrscheinlichkeitsverteilung der Zielgröße des Unternehmens (z. B. Gewinn oder Cashflow) zusammengeführt. Aus dieser können dann Risikomaße für das Gesamtunternehmen berechnet werden, die den Gesamtrisikoumfang charakterisieren.

Die Beurteilung des Gesamtrisikoumfangs ermöglicht eine Aussage darüber, ob die Risikotragfähigkeit eines Unternehmens ausreichend ist, um den Risikoumfang des Unternehmens tatsächlich zu tragen und damit den Bestand des Unternehmens langfristig zu gewährleisten. Sollte der vorhandene Risikoumfang eines Unternehmens gemessen an der Risikotragfähigkeit zu hoch sein, werden zusätzliche Maßnahmen der Risikobewältigung erforderlich.

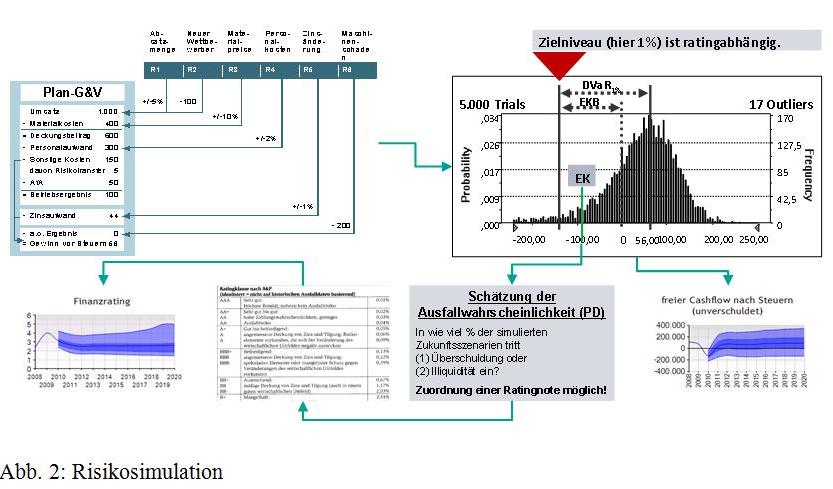
Bei der Risikoaggregation werden mittels Simulation die durch Wahrscheinlichkeitsverteilungen beschriebenen Risiken in den Kontext der Unternehmensplanung gestellt, d. h. es wird jeweils aufgezeigt, welches Risiko an welcher Position der Planung (Erfolgsplanung) zu Abweichungen führen kann. Mit Hilfe von Risikosimulationsverfahren (Monte-Carlo-Simulation) kann dann eine große repräsentative Anzahl möglicher risikobedingter Zukunftsszenarien berechnet und analysiert werden. Damit sind Rückschlüsse auf den Gesamtrisikoumfang, die Planungssicherung und die realistische Bandbreite, z. B. des Unternehmensergebnisses, möglich.

Die Monte-Carlo-Simulation liefert eine große „repräsentative Stichprobe“ der risikobedingt möglichen Zukunftsszenarien des Unternehmens, die dann analysiert wird. Aus den ermittelten Realisationen der Zielgröße (z. B. Gewinn) ergeben sich aggregierte Häufigkeitsverteilungen. Ausgehend von der Häufigkeitsverteilung der Gewinne kann man unmittelbar auf die Risikomaße, wie z. B. den Eigenkapitalbedarf (RAC) des Unternehmens, schließen (vgl. Abschnitt 6). Zur Vermeidung einer Überschuldung wird nämlich zumindest so viel Eigenkapital benötigt, wie auch Verluste auftreten können, die dieses aufzehren.

Bei bisher beschriebenen Risikoaggregationsmodellen wird immer zunächst von der Unternehmensplanung ausgegangen. Dabei existieren zwei (kombinierbare) Varianten der Risikoerfassung, nämlich

- die unmittelbare Berücksichtigung der Planungsunsicherheit bei den einzelnen Planungspositionen (d. h. das Beschreiben einer Planungsposition durch eine Verteilung, z. B. eine Normalverteilung) oder

- die separate quantitative Beschreibung eines Risikos durch eine geeignete Verteilungsfunktion (z. B. durch Schadenshöhe und Eintrittswahrscheinlichkeit bei ereignisorientierten Risiken) und die Zuordnung dieses Risikos in einem zweiten Schritt zu der Planungsposition, wo es Planabweichungen auslösen kann.

Mit dem „Risikofaktorenansatz“ gibt es eine weitere, ebenfalls kombinierbare Variante zur Berücksichtigung von Risiken im Kontext der Planung. Neben der Unternehmensplanung wird dabei ein Modell der Unternehmensumwelt mit den für das Unternehmen interessanten Variablen aufgebaut (z. B. Bartram, 1999). Die Unternehmensumwelt wird dabei beispielsweise durch exogene Faktoren beschrieben wie Wechselkurse, Zinssätze, Rohstoffpreise und Konjunktur (z. B. zur Nachfrage-Wachstumsrate). Für alle diese exogenen Faktoren des Unternehmensumfeldes werden Prognosen erstellt, so dass ein „Plan-Umfeldszenario“ entsteht. Die Abhängigkeit der Planvariablen des Unternehmens von exogenen Faktoren wird z. B. durch Elastizitäten erfasst. Diese zeigen, welche Konsequenzen eine (unsichere) Änderung des Risikofaktors für die Plan-Variable (z. B. Umsatz) hat.

Risikomaße

Grundlagen Sollen Entscheidungen unter Unsicherheit (Risiko) getroffen werden, müssen die Handlungsalternativen auch hinsichtlich ihres Risikogehalts bewertet werden. Risikomaße ermöglichen den Vergleich unterschiedlicher Risiken mit unterschiedlichen Charakteristika, Verteilungstypen, Verteilungsparametern (wie beispielsweise Schadenshöhe).

Das traditionelle Risikomaß der Kapitalmarkttheorie (CAPM, Markowitz-Portfolio) stellt die Varianz bzw. die Standardabweichung – als Wurzel der Varianz – dar. Varianz und Standard-abweichung sind Volatilitätsmaße, d. h., sie quantifizieren das Ausmaß der Schwankungen einer risikobehafteten Größe um die mittlere Entwicklung (Erwartungswert).

Varianz bzw. Standardabweichung sind relativ einfach zu berechnen und leicht verständlich. Allerdings berücksichtigen sie sowohl die negativen als auch die positiven Abweichungen vom erwarteten Wert. Investoren sind meistens aber eher an den negativen Abweichungen interessiert. So genannte Downside-Risikomaße beruhen dagegen auf der Idee, dass das (bewertungsrelevante) Risiko als mögliche negative Abweichung von einem erwarteten Wert angesehen wird und berücksichtigen somit lediglich diese. Hierzu gehören beispielsweise der Value-at-Risk, der Conditional Value-at-Risk oder die untere Semivarianz (ein LPM2-Risikomaß).

Risikomaße lassen sich auf verschiedene Art und Weise klassifizieren. Zum einen nach der Lageabhängigkeit. Lageunabhängige Risikomaße (wie beispielsweise die Standardabweichung) quantifizieren das Risiko als Ausmaß der Abweichungen von einer Zielgröße. Lageabhängige Risikomaße wie beispielsweise der Value-at-Risk hingegen sind von der Höhe des Erwartungswerts abhängig. Häufig kann ein solches Risikomaß als „notwendiges Eigenkapital“ bzw. „notwendige Prämie“ zur Risikodeckung angesehen werden (vgl. Abschnitt 6.2).

Dabei können die beiden Arten ineinander umgeformt werden. Wendet man beispielsweise ein lageabhängiges Risikomaß nicht auf eine Zufallsgröße X (z. B. Gewinn), sondern auf eine zentrierte Zufallsgröße X-E(X)an, so ergibt sich ein lageunabhängiges Risikomaß. Da in die Berechnung von lageabhängigen Risikomaßen auch die Höhe des Erwartungswerts einfließt, können diese auch als eine Art risikoadjustierter Performancemaße interpretiert werden.

Der wesentliche Vorteil eines lageunabhängigen Risikomaßes besteht darin, dass hier die „Höheninformation“ (erwartetes Ergebnis) und die „Risikoinformation“ (Abweichung) klar getrennt werden, so dass die Achsen in einem Rendite-Risiko-Portfolio unabhängig voneinander sind. Lageabhängige Risikomaße entsprechen dagegen mehr dem intuitiven Risikoverständnis, da hier bei ausreichend hohen „erwarteten Renditen“ die möglichen Abweichungen an Bedeutung verlieren, da sie nicht mehr so stark zu einem möglichen Unterschreiten der Zielgröße (z. B. erwartete Mindestrendite) führen.

Der Value-at-Risk (VaR), als lageabhängiges Risikomaß, berücksichtigt explizit die Konsequenzen einer besonders ungünstigen Entwicklung für das Unternehmen. Er ist definiert als Schadenshöhe, die in einem bestimmten Zeitraum („Halteperiode“, z. B. ein Jahr) mit einer festgelegten Wahrscheinlichkeit p (z. B. aus vorgegebenem Zielrating) nicht unterschritten wird. Formal gesehen ist ein Value-at-Risk somit das negative Quantil Q einer Verteilung.

Das lageunabhängige Gegenstück zum Value-at-Risk ist der Deviation Value-at-Risk (DVaR, oder auch relativer VaR), der sich als Value-at-Risk von X-E(X) ergibt.

Der Value-at-Risk (und der Eigenkapitalbedarf EKB, der als VaR bezogen auf den Unternehmensgewinn aufgefasst werden kann) ist ein Risikomaß, das nicht die gesamten Informationen der Wahrscheinlichkeitsdichte berücksichtigt. Welchen Verlauf die Dichte unterhalb des gesuchten Quantils nimmt, also im Bereich der Extremwirkungen (Schäden), ist für den Eigenkapitalbedarf unerheblich. Damit werden aber Informationen vernachlässigt, die von erheblicher Bedeutung sein können.

Im Gegensatz dazu berücksichtigen die Shortfall-Risikomaße – und insbesondere die so genannten Lower Partial Moments (LPMs) – gerade die oft zur Risikomessung interessanten Teile der Wahrscheinlichkeitsdichte von minus unendlich bis zu einer gegebenen Zielgröße (Schranke c). Das Risikoverständnis entspricht der Sichtweise eines Bewerters, welcher die Gefahr des Shortfalls, der Unterschreitung eines von ihm festgelegten Ziels (z. B. geforderte Mindestrendite) in den Vordergrund stellt. Allgemein berechnet sich ein LPM-Maß der Ordnung m durch

Üblicherweise werden in der Praxis drei Spezialfälle betrachtet, nämlich die Shortfallwahrscheinlichkeit (Ausfallwahrscheinlichkeit), d. h. m=0, der Shortfallerwartungswert (m=1) und die Shortfallvarianz (m=2). Im Gegensatz zur Varianz werden beispielsweise bei der unteren Semivarianz nur negative Abweichungen vom erwarteten Wert in die Berechnung einbezogen.

Die erwähnte Ausfallwahrscheinlichkeit p (PD, Probability of Default), ein LPM-Maß der Ordnung 0, gibt die Wahrscheinlichkeit an, dass eine Variable (wie beispielsweise das Eigenkapital) einen vorgegebenen Grenzwert (hier meist Null) unterschreitet, und charakterisiert damit ein Rating (vgl. Gleißner 2011).

Berücksichtigung von Risikoinformationen in Performancemaßen und wertorientierter Steuerung

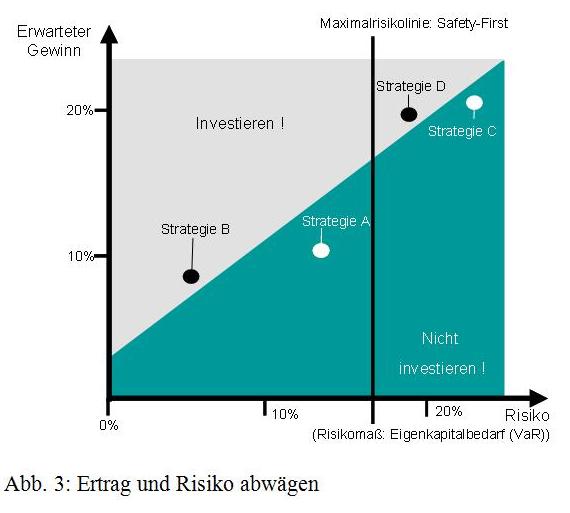
Es ist das zentrale Anliegen einer wertorientierten Unternehmensführung, dass bei der Vorbereitung unternehmerischer Entscheidungen die zu erwartenden Erträge und Risiken gegenei-nander abgewogen werden. Die folgende Abbildung verdeutlicht diese Grundidee.

Durch die Identifikation, quantitative Beschreibung und Aggregation der Risiken eines Projektes kann der Gesamtrisikoumfang (auf der x-Achse), z. B. ausgedrückt im Eigenkapitalbedarf (VaR), den erwarteten Erträgen des Projektes gegenübergestellt werden. Diese Quantifizierung der Risiken ermöglicht es zunächst zu überprüfen, ob der mit dem Projekt verbundenen aggregierte Gesamtrisikoumfang vom Unternehmen getragen werden kann (Maximalrisikolinie, abgeleitet aus Eigenkapital- und Liquiditätsreserven, d. h. Risikotragfähigkeit).

Zudem erfordert ein höherer Risikoumfang einen höheren zu erwartenden Gewinn (oder höhere Rendite), d. h. die Projekte sollten ein günstiges Ertrags-Risiko-Profil aufweisen, um die Durchführung bzw. Investition zu rechtfertigen.

Will man die Positionierung eines Projektes oder Unternehmens aus dem Rendite-Risiko-Diagramm gemäß Abbildung 7 durch eine Kennzahl ausdrücken, gelangt man unmittelbar zu den Performancemaßen. Ein Performancemaß ergibt sich durch die Kombination des Erwar-tungswerts des Ergebnisses (z. B. des Gewinns) mit einem zugehörigen Risikomaß.

Eine Performancemessung kann ex ante oder ex post durchgeführt werden. Ein ex ante Performancemaß dient dabei als prognostizierter Erfolgsmaßstab der Entscheidungsvorbereitung für (oder gegen) eine unternehmerische Aktivität, z. B. eine Investition. Dabei wird der Unsicherheit jeder Zukunftsprognose (über eine Zielgröße X), die Grundlage der ökonomischen Entscheidung ist, explizit Rechnung getragen. Solche Performancemaße sind daher Kennzahlen, die sich aus der Kombination (operationalisiert durch eine Funktion f) des erwarteten Ergebnisses E(X) (z. B. erwarteter Gewinn) mit einem geeigneten Risikomaß R(X) wie Standardabweichung oder Value at Risk ergeben. Das Risikomaß zeigt dabei den Umfang möglicher Planabweichungen.

Im einfachsten Fall ergibt sich das Performancemaß P(X) für den unsicheren Gewinn X indem man den Erwartungswert E(X) durch einen Risikoabschlag reduziert, der unmittelbar abhängig ist vom Risikomaß R(X), also z. B. vom Value-at-Risk (des Gewinns) bzw. des Eigenkapitalbedarfs. Beispiel:

Das Abziehen des Risikoabschlags vom Erwartungswert entspricht dem Vorgehen bei der Bestimmung sogenannter „Sicherheitsäquivalente“, die ausdrücken, welche sicheres Ergebnis aus Sicht des Bewertenden äquivalent ist zum unsicheren Ertrag X. Wählt man als Risikomaß beispielsweise den Eigenkapitalbedarf, kann man die Größe , den „Preis des Risikos“, interpretieren als kalkulatorische (Zusatz-) Kosten für das Eigenkapital. Damit entspricht der Risikoabschlag gerade den kalkulatorischen Eigenkapitalkosten oder Wagniskosten.

Zu den Performancemaßstäben gehören Unternehmenswert (Kapitalwert), Wertbeitrag (EVA) und RoRAC oder auch das Sharpe Ratio (SR).

Als Alternative zum Sharpe Ratio sind Performancemaße anzusehen, bei denen Überschussrendite (im Bezug zur risikolosen Anlage) ins Verhältnis gesetzt wird zu LPM-Risikomaßen. Derartige Performancekennzahlen werden bezeichnet als „Return to Shortfall“ (RTS) Kennzahlen.

Auch der Unternehmenswert ist als Performancemaß interpretierbar, weil sich dieser ergibt durch die risikogerechte Diskontierung der zukünftig erwarteten Erträge oder Cashflows. Um den modellbasiert berechneten Wert als Performancemaß auffassen zu können, ist es allerdings notwendig, den Diskontierungszinssatz (oder Kapitalkostensatz) tatsächlich aus den zukünftigen Risiken abzuleiten – und nicht etwa aus historischen Kapitalmarktdaten (Aktienrenditen), wie beispielsweise im Rahmen des sogenannten Capital Asset Pricing Modells. Bei diesem Vorgehen kann man den Diskontierungszinssatz (die Kapitalkosten) als risikogerechte Anforderungen an die Rendite eines Projektes oder Unternehmens auffassen, d. h. mit der Berechnung von Kapitalkosten wird der Risikoumfang als Renditeanforderung dargestellt. Ein höherer Umfang von Risiken führt zu potentiell höheren (negativen) Planabweichungen bzw. Verlusten, was einen höheren „Eigenkapitalbedarf“ und damit höhere Kapitalkosten mit sich bringt.

Ein Performancemaß, das sich auch als lageunabhängiges Risikomaße auffassen lässt, ist RAVA. RAVA steht für „Risk Adjusted Value Added“. Im Gegensatz zu den heute üblichen Performance-Maßen, wie EVA (Economic Value Added), wird bei diesem Performancemaß tatsächlich eine adäquate und planungskonsistente Risikoerfassung vorgenommen (Gleißner 2011).

RAVA reduziert also den erwarteten Gewinn (erwartetes Betriebsergebnis E(X) abzüglich risikoloser Verzinsung des eingesetzten Kapitals, CE, um einen Risikoabschlag. Als Risikomaß wird hier üblicherweise der Eigenkapitalbedarf herangezogen:

Die Anwendung des Performancemaßes RAVA ist einfach. In dem kleinen Fallbeispiel zur Risikoaggregation (Abschnitt 5) wurde ein erwarteter Gewinn des Unternehmens von 0,33 Mio. Euro und ein „Eigenkapitalbedarf“ von 1,4 Mio. Euro (Value-at-Risk zum 5%-Niveau) bestimmt. Geht man (vereinfachend) von einem Risikozuschlag für das Eigenkapital von 10% aus, sind bei der „Performancebeurteilung“ des Unternehmens damit kalkulatorische Eigenkapitalkosten von 10% x 1,4 Mio. Euro, also 0,14 Mio. Euro zu berücksichtigen.

Entsprechend berechnet sich für RAVA: RAVA = erwarteter Gewinn – 10% x Eigenkapitalbedarf = 0,33 – 10% x 1,4 = 0,19 Mio Euro.

Literatur

Albrecht, P. / Maurer, R., Investment- und Risikomanagement, 2005.

Artzner, P. / Delbaen, F. / Eber, J.-M. / Heath, D., Coherent Measures of Risk, in: Mathematical Finance, Juli / 1999, S. 203 – 228.

Baule, R. / Ammann, K. / Tallau, Ch., Zum Wertbeitrag des finanziellen Risikomanagements, in: WiSt – Wirtschaftswissenschaftliches Studium, 2 / 2006, S. 62 – 65.

Gleißner, W., Unternehmenswert, Rating und Risiko, in: WPg Die Wirtschaftsprüfung, 14/2010, 63. Jg., S. 735 – 743.

Gleißner, W., Grundlagen des Risikomanagements im Unternehmen, 2. Aufl., 2011.

Gleißner, W., Risikoanalyse und Replikation für Unternehmensbewertung und wertorientierte Unternehmenssteuerung, in: WiSt, 7 / 11, S. 345 – 352.

Gleißner, W. / Lenz, A. / Tilch, T., Risikogerechte Beteiligungsbewertung - Die Bedeutung von Wertanalysen im gesetzlichen Kontext, in: ZfCM | Controlling & Management, S. 158 – 164.

Pedersen, C. / Satchell, S., An Extended Family of Financial-Risk Measures, in: Geneva Papers of Risk and Insurance 1998, S. 89 – 117.

Rockafellar, T. / Uryasev, S. / Zabarankin, M., Deviation Measures in Risk Analysis and Optimization, in: Research Report 12 / 2002, S. 1 – 27.

Zeder, M., Extreme Value Theory im Risikomanagement, 2007.

Ersteinstellender Autor

Dr. Werner Gleißner, FutureValue Group, [1]